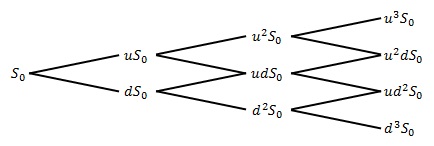期权定价
期权指的是一种在一定期限内的交易选择权,也就是赋予了持有人一种按照约定价格买或卖的权利,但是持有人可以自己决定要不要行使这个权利。期权定价中,从简单的二项式期权定价模型开始,说明这一方法如何逐步转化为精确实用的布莱克-斯科尔斯模型(B-S-M模型)。
一、期权分类
1、按期权的交割时间划分,有美式期权(American Option)和欧式期权(European Option)两种类型。美式期权是指在期权合约规定的有效期内任何时候都可以行使权利。欧式期权是指在期权合约规定的到期日方可行使权利,期权的买方在合约到期日之前不能行使权利,过了期限,合约则自动作废。
2、按期权合约上的标的划分,有股票期权、股指期权、利率期权、商品期权以及外汇期权等种类。
3、按期权的权利划分,有看涨期权和看跌期权两种类型。
(1)看涨期权(Call Options),期权的买方支付权利金于卖方后,即拥有在期权合约的有效期内,按执行价格向期权卖方买入一定数量标的物的权利,但不负有必须买进的义务;期权的卖方缴交保证金于交易所防止违约,即有义务在期权规定的有效期内,应期权买方的要求,按执行价格卖出相应数量标的物。
(2)看跌期权(Put Options),期权的买方支付权利金与卖方后,即拥有在期权合约的有效期内,按执行价格向期权卖方卖出一定数量标的物的权利,但不负有必须卖出的义务。期权的卖方缴交保证金于交易所防止违约,即有义务在期权规定的有效期内,应期权买方的要求,按执行价格买入相应数量标的物。
期权的构成要素:
(1)执行价格(strike price),期权的买方行使权利时事先规定的标的物买卖价格;
(2)权利金(premium),期权的买方支付的期权价格,即买方为获得期权而付给期权卖方的费用;
(3)保证金(margin),期权卖方必须存人交易所用于履约的财力担保。
二、期权基本交易策略
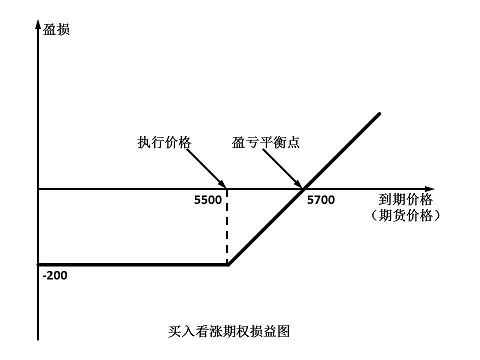
1、买入看涨期权
(1)运用场合
a、后市大涨。越是看大涨,越可以用虚值看涨期权,以捕捉价格急升所可能带来的利润;
b、市场波幅正在扩大;
c、愿意利用买进期权的优势,即有限风险的杠杆作用;
d、预期后市看涨,但不愿意付出更多保证金买进标的物;
e、牛市,但隐含价格波动率低(理论上应该波动较大,但市场反应较小,因此在牛市时买入被市场低估的看涨期权)。
(2)收益
a、平仓收益 = 权利金卖出价 – 权利金买入价;
b、履约收益 = 标的物价格 – 执行价格 – 权利金。
(3)最大风险:损失全部权利金
(4)损益平衡点:执行价格+权利金
(5)时间价值的损耗:随着合约时间的减少,时间价值会一直下跌。如果波幅上升,时间价值下跌较慢;如果波幅下跌,时间价值的损耗加速。
(6)保证金:不交
(7)履约部位:多头
例1:白糖期货价格为5300元/吨,某投资者十分看淡白糖期货后市,卖出一手执行价格为5500元/吨的白糖看涨期权,收入权利金200元/吨。损益平衡点为5700元/吨。若10天后,白糖期货价格涨至5600元/吨,看涨期权跌至100元/吨,投资者买入平仓,获利100元/吨;若保留至到期日,白糖期货价格只要维持在5500元/吨以下,买方均会放弃执行的权利,投资者可以获取200/吨的利润。
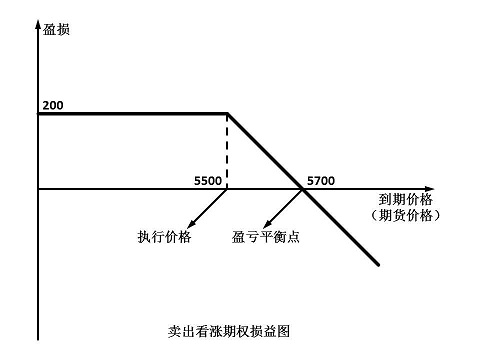
2、卖出看涨期权
(1)运用场合
a、看后市下跌或已见顶。深信大势已见顶,会辗转下跌,更可卖出实值看涨期权,以赚取最大的利润。否则,宜卖出平值或虚值看涨期权。
b、市场波幅收窄。
c、已经持有现货或期货合约,作为对冲策略。、
d、熊市,隐含价格波动率高。
(2)最大收益
a、平仓收益 = 权利金卖出价 – 权利金买入平仓价;
b、期权被放弃的收益 = 所收取的全部权利金。
(3)风险
a、斩仓风险 = 权利金卖出价 – 斩仓买入价啊;
b、期权被要求履约风险 = 执行价格 – 标的物平仓买入价格 + 权利金。
(4)盈损平衡点:执行价格 + 权利金
(5)时间价值的损耗:时间越近到期日,价格又在执行价格左右,卖方的收益最大。
(6)保证金:下列两者较大者
a、权利金 + 期货合约的保证金 – 虚值期权价值的一半;
b、权利金 + 期货合约保证金一半。
(7)履约部位:空头
例2:白糖期货价格为5300元/吨,某投资者十分看淡白糖期货后市,卖出一手执行价格为5500元/吨的白糖看涨期权,收入权利金200元/吨。损益平衡点为5700元/吨。若10天后,白糖期货价格涨至5600元/吨,看涨期权跌至100元/吨,投资者买入平仓,获利100元/吨;若保留至到期日,白糖期货价格只要维持在5500元/吨以下,买方均会放弃执行的权利,投资者可以获取200/吨的利润。
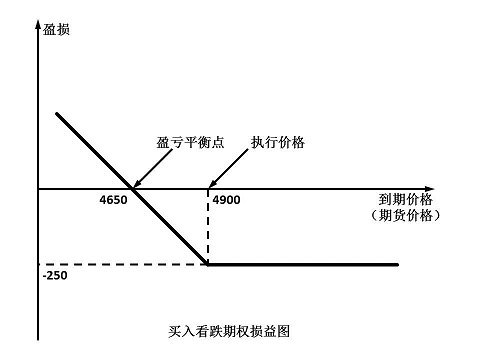
3、买入看跌期权
(1)运用场合
a、看后市将要大跌或正在下跌。越是看大跌,越可以用虚值看跌期权,以捕捉价格急跌所带来的利润。
b、市场波幅正在扩大。
c、熊市,隐含价格波动率低。
(2)收益
a、平仓收益=权利金卖出平仓价-买入价;
b、履约收益=执行价格-标的物价格-权利金。
(3)最大风险:损失全部权利金
(4)盈损平衡点:执行价格-权利金
(5)时间价值的损耗:时间会一直下跌。如果波幅上升,时间价值下跌较慢;如果波幅下跌,时间价值的损耗加速。
(6)保证金:不交
(7)履约部位:空头
例3:白糖期货价格为5150元/吨,某投资者十分看空白糖期货后市,买入一手执行价格为4900元/吨的白糖看跌期权,支出权利金250元/吨。损益平衡点为4650元/吨。若10天后,白糖期货价格跌至4800元/吨,看跌期权涨至400元/吨,投资者卖出平仓,获利150元/吨。
4、卖出看跌期权
(1)运用场合
a、看后市上涨或已见底。如坚信后市看涨,可卖出看跌期权收取权利金。如深信大势见底,会辗转上涨,更可卖出实值看跌期权,以赚取最大的利润;否则,只宜卖出平值或虚值看跌期权。
b、市场波幅收窄的市况。
c、隐含价格波动率高。
(2)最大收益
a、平仓收益=权利金卖出价-买入平仓价;
b、期权被放弃的收益=所收取的权利金。
(3)风险
a、斩仓风险=权利金卖出价-买入斩仓价;
b、期权被要求履约风险=标的物卖出平仓价-执行价格+权利金。
(4)盈亏平衡点:执行价格-权利金
(5)时间价值损耗:时间越是接近到期日,价格又在执行价格左右,卖家的收益越大。
(6)保证金:下列两者较大者
a、权利金+期货合约的保证金-虚值期权价值的一半;
b、权利金+期货合约保证金一半。
(7)履约部位:多头
例4:白糖期货价格为5150元/吨,某投资者谨慎看好白糖期货后市,卖出一手执行价格为4900元/吨的白糖看跌期权,收入权利金250元/吨。损益平衡点为4650元/吨。若10天后,白糖期货价格跌至4800元/吨,看跌期权跌至150元/吨,投资者买入平仓,获利100元/吨;若保留至到期日,白糖期货价格只要维持在4900元/吨以上,买方均会放弃执行的权利,投资者可以获取250/吨的利润。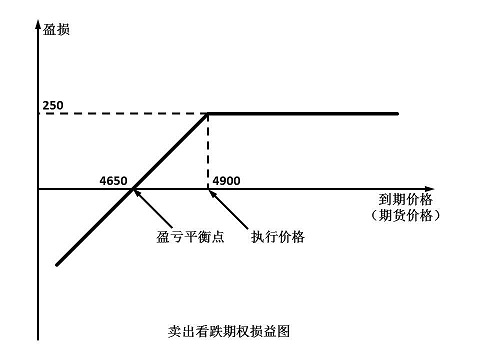
三、期权定价
1、内在价值与时间价值
内在价值(intrinsic Value)指立即履行合约时可获取的总利润。具体来说,可以分为实值期权、虚值期权和平值期权。
(1)实值期权(in the money option):当看涨期权的执行价格低于当时的实际价格时,或者当看跌期权的执行价格高于当时的实际价格时,该期权为实值期权,执行价格与实际价格之差,即为实值期权的内在价值;
(2)虚值期权(out of the money option):当看涨期权的执行价格高于当时的实际价格时,或者当看跌期权的执行价格低于当时的实际价格时,该期权为虚值期权,内在价值为零;
(3)平值期权(at the money option):当看涨期权的执行价格等于当时的实际价格时,或者当看跌期权的执行价格等于当时的实际价格时,该期权为平值期权,内在价值为零。
考虑某时刻处于虚值状态的看涨期权,这时股票价格低于执行价格。这并不意味着期权毫无价值(权利金)。即使现在执行期权无利可图,但期权价值(权利金)仍为正,因为在到期时刻股票价格有可能上涨到足以使执行期权变得有利可图。否则,最坏的结果不过是期权以零值失效。
由此可见,虽然虚值期权和平值期权没有内在价值,但是含有时间价值。在期权语境中,时间价值仅是指期权价格与期权被立即执行时价值之间的差。它是期权价值(权利金)的一部分,来源于期权距离到期日还有一段时间。
期权的大部分时间价值是一种典型“波动性价值”。因为期权持有者可以选择不执行期权,收益最低也就是零。虽然看涨期权现在处于虚值,但仍然具有正的价格,因为一旦股票价格上涨,就存在潜在的获利机会,而在价格下跌时不会带来更多损失的风险。波动性价值依赖于当选择执行无利可图时可以选择不执行的权利。执行权力,而不是履行义务,期权为较低的股票价格表现提供了保险。
期权价格(权利金)=内在价值+时间价值
2、期权价格的决定因素
我们可以确定影响期权价值(权利金)的因素至少有六个:股票价格、执行价格、股票价格的波动性、到期期限、利率和股票的股息率。
看涨期权价值(权利金)与股票价格同向变动,而与执行价格反向变动,因为股票期权被执行,其收益等于${S_T} – X$。看涨期权期望收益的幅度随${S_0} – X$的增加而增加。
看涨期权价值(权利金)也随着股票价格波动性的增加而增加。为了解释这个问题,假设存在两种情形,一种是到期日股票价格可能在10~50美元变化,另一种则在20~40美元变化。这两种情形下,股票价格期望值或平均值均为30美元。假定看涨期权的执行价格为30美元,期权的损益各是多少?
| 高波动性情形(美元) | |||||
| 股票价格 | 10 | 20 | 30 | 40 | 50 |
| 期权损益 | 0 | 0 | 0 | 10 | 20 |
| 低波动性情形(美元) | |||||
| 股票价格 | 20 | 25 | 30 | 35 | 40 |
| 期权损益 | 0 | 0 | 0 | 5 | 10 |
如果每种结果出现的可能性都相同,概率都为20%,高波动性情形下期权的期望损益为(10+20)/5=6美元,而低波动性情形下期权的期望损益只有(5+10)/5=3美元。
尽管在上述两种情形下,股票的平均价格都是30美元,但是高波动性情形下期权的平均损益更高。这一额外价值源于期权持有者所承受的损失都是有限的,或者说是看涨期权的波动性价值。不管股票价格从30美元跌至何处,持有者得到的均为零。显然,对看涨期权持有者来说,股票价格表现不好时,跌多跌少没有什么不同。
但是,当股票价格表现较好的情况下,看涨期权到期时就会变成实值期权,并且股价越高,期权的收益就越大。这样,极好的股票表现带来的收益是无限的,极差的股票表现也不会使期权的收益降至零之下。这种不对称性意味着标的股票价格波动性的增加使期权的期望收益增加,从而增加了期权价格(权利金)。
同样,到期期限越长,看涨期权价值(权利金)也越大。期限越长,发生影响股票价格的不可预测时间的机会越多,从而导致股票价格可能上升的范围更大。这与波动性增加的效果是相似的。而且,随着到期期限的延长,执行价格现值下降,这也有利于看涨期权的持有者,增加了期权价值(权利金)。
由此可以推出,利率上升时,看涨期权价值(权利金)增加,因为高利率降低了执行价格的现值。
最后,公司的股利政策也影响期权价值(权利金)。高额股利政策会降低股票价格的增长率。对于任何股票的期望收益来说,股利支付越高意味着期望资本收益率越低。对股票价格估值的抑制也降低了看涨期权的潜在收益,从而降低了期权的价值。
| 看涨期权价值(权利金)的决定因素 | |
| 如果该变量增大 | 看涨期权价值(权利金) |
| 股票价格,$S$ | 增加 |
| 执行价格,$X$ | 降低 |
| 波动性,$\sigma $ | 增加 |
| 到期时间,$T$ | 增加 |
| 利率,${r_f}$ | 增加 |
| 股利支付 | 降低 |
3、二项式期权定价
没有坚实的数据基础,要完全理解通常使用的期权定价公式是很困难的。但是,我们仍然可以通过一个简单的特例来对期权定价进行有价值的考察。假定在期权到期时股票价格只有两种可能的值:股票价格涨到给定的较高价格,或者降到给定的较低价格。虽然这可能看起来太简单,但可以帮助我们进一步理解更复杂与现实的模型。而且,我们可以拓展此模型来描述股票价格行为更合理的特征。
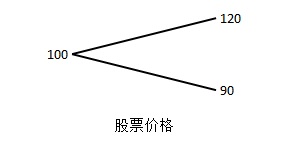
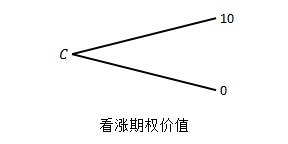
假定年初股票价格为100美元,年底的股票价格有两种可能,上涨$u = 1.20$至120美元($u$表示上涨)或者下跌$d = 0.90$至90美元($d$表示下跌)。该股票的看涨期权的执行价格为110美元,到期期限为1年。利率为10%。如果股票价格下跌,年底看涨期权持有者的收益率为零;如果上涨到了120美元,收益率为10美元。
下面用“二叉树”来阐述这些可能性:
一股股票与该股票的抵押借款构成资产组合,借款利率10%,按照最低的可能到期股价,即90美元借款,实际到手90/1.1=81.82美元。
| 年底的股票价格 | 90 | 120 |
| -贷款的本金和利息 | -90 | -90 |
| 总计 | 0 | 30 |
若年底股价跌至90美元,则实际亏损18.18美元(其中10美元为股票亏损,8.18美元为借款利息),承担亏损18.18美元的风险,获得的收益为0或30美元。
若将看涨期权与上述组合进行比较,不管年底股票价格是何值,组合的收益都是看涨期权收益的三倍。换句话说,三份看涨期权正好可以复制出股票抵押借款的收益;于是三份看涨期权的价值与构建资产组合的成本相同。这样,三份看涨期权的售价应等于资产组合的成本,即$3C = 18.18$美元,每份看涨期权的售价为6.06美元。这样,给定股票价格、执行价格、利率与股票价格波动性(即股票价格上涨或下跌的幅度),我们就能够得出看涨期权的公允价值。
这种定价方法主要依赖于复制的概念。基于股票以后两种可能的价值,资产组合的收益复制了三份看涨期权的收益,因此具有相同的市场价格。复制已成为大部分期权定价公式的后盾。对于几个分布更复杂的股票来说,复制技术也相应的更为复杂,但原理是相同的。
我们也可以从另一个角度来考察复制的作用。仍使用前面例子的数据,由一股股票和出售三份看涨期权构成的资产组合是完全对冲的。它的年末价值不受最终股票价格影响:
| 年底的股票价格 | 90 | 120 |
| -出售三份看涨期权的义务 | -0 | -30 |
| 总计 | 90 | 90 |
投资者构建了一个无风险资产组合,其未来收益为90美元。它的价值一定等于90美元的现值,即90/1.1=81.82美元。资产组合的价值,等于股票多头100美元减去卖出三份看涨期权的价值$3C$,应该等于81.82美元。因此$100 – 3C = 81.82$美元,即$C = 6.06$美元。
这个例子中的对冲比率是一股股票对三份看涨期权,即1:3。对出售的每份看涨期权而言,资产组合中必须保持1/3股股票来对冲风险。这个比率在这里简单解释如下:它是期权价值的变动范围与股价只有两个取值时的股价变动范围的比值。对冲比率等于变动范围的比率,因为在这个两状态例子中,期权与股票是完全相关的。当期权与股票完全相关时,完全对冲要求持有期权与股票的比例由相对波动性来决定,其公式为:
$$H = \frac{{{C_u} – {C_d}}}{{u{S_0} – d{S_0}}}$$
其中,${{C_u}}$和${{C_d}}$分别表示股票价格上涨与下跌时看涨期权的价值,${u{S_0}}$和${d{S_0}}$是两状态下的股票价格。对冲比率$H$是期权与股票期末价值波动范围的比率。如果投资者出售一份期权,并持有$H$股股票,那么该资产组合的价值将不受股票价格的影响。在这种情况下,期权定价就很容易,仅仅使对冲的资产组合的价值等于已知收益的现值即可。
利用上述例子,期权定价技术将包括以下步骤:
(1)给定年底可能的股票价格,$u{S_0} = 120$和$d{S_0} = 90$,执行价格为110,计算得${C_u} = 10$和${C_d} = 0$。股票价格变动范围30,期权价格变动范围为10;
(2)计算对冲比率为10/30=1/3;
(3)卖出一份期权与买入1/3股股票组成的资产组合在年末的价值确定为90/3=30美元;
(4)年利率为10%,30美元的现值为30/1.10=27.27美元;
(5)让对冲头寸的价值等于将来确定收益的现值:$1/3{S_0} – {C_0} = 27.27$(美元);
(6)解出看涨期权的价格,${C_0} = 6.06$美元。
如果期权价格被高估(比如售价为6.50美元)又会如何呢?这样就可以有套利空间,具体做法为:
| 初始现金流 | 对每种可能的股票价格一年后的现金流 | ||
| ${S_0} = 100$ | ${S_1} = 90$ | ${S_1} = 120$ | |
| 卖出3份看涨期权 | 19.50 | 0 | -30 |
| 买入1股股票 | -100 | 90 | 120 |
| 以年利率10%借入80.50美元 | 80.5 | -88.55 | -88.55 |
| 总计 | 0 | 1.45 | 1.45 |
虽然初始净投资为零,但一年后的收益为正,并且是无风险的。如果期权价格被低估了,就可以采用相反的套利策略:买入看涨期权,卖出股票,消除价格风险。另外,套利利润的现值正好等于期权价值高估部分的3倍。利率10%,无风险利润1.45的现值是1.318美元。该套利策略卖出了3份看涨期权,给每份期权带来0.44美元的利润,正好等于期权价值被高估的数额:6.50美元减去公允价值6.06美元。
4、二项式方法的推广
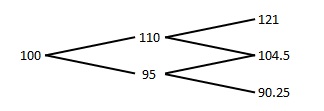
虽然二项式期权定价模型看起来很简单,但是可以将其推广,加入现实的假设。首先,我们假定将一年分成两个6个月,然后假定在任何一个时期,股票都只有两个可能的价格。这里我们假定股价将上涨10%(即$u = 1.10$)或下降5%(即$d = 0.95$)。股票的初始价格为每股100美元,在一年中价格可能的路径为:
中间价为104.5美元,可通过两条途径获得:上涨10%后下跌5%,或者下跌5%后上涨10%。
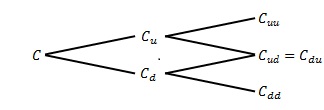
这里有三种可能的年末股票价值与期权价值:
使用类似前面采用的方法,可以从${C_{uu}}$和${C_{ud}}$得到${C_{u}}$,从${C_{du}}$和${C_{dd}}$得到${C_{d}}$,然后从${C_{u}}$和${C_{d}}$得到$C$。以此类推,间隔时间可以不用局限于6个月,可以把1年分成4个3个月,12个1个月或者365天,每一个时间段都假定是一个二项式过程。
例5:假定6个月无风险利率为5%,有一个执行价格为110美元的股票看涨期权,用上述二项式期权定价模型来对此期权进行定价。
首先对${C_{u}}$的价值入手,从这点开始,知道期权的到期日,看涨期权期权价值能上涨至${C_{uu}} = 11$美元(因为在该点股票价格$u \times u \times {S_0} = 121$美元)或者下跌至${C_{ud}} = 0$(因为在该点股票价格$u \times d \times {S_0} = 104.5$美元,低于期权执行价格110美元)。因此,在该点的对冲比率为:
$H = \frac{{{C_{uu}} – {C_{ud}}}}{{uu{S_0} – ud{S_0}}} = \frac{{11 – 0}}{{121 – 104.5}} = 2/3$
这样,不管到期日股票价格如何,下列资产组合的价值都为209美元:
| $ud{S_0} = 104.5$美元 | $uu{S_0} = 121$美元 | |
| 以$u{S_0} = 110$美元的价格买入2股股票 | 209 | 242 |
| 以价格${C_u}$卖出3份看涨期权 | 0 | -33 |
| 总计 | 209 | 209 |
该组合的当前市场价值等于209美元的现值:
$2 \times 110 – 3{C_u} = 209/1.05 = 199.0476$美元
由上式可以求得${C_u} = 6.9841$美元。
下一步,求${C_d}$的价值,相应股票价格为95美元,期权到期日股票价格为104.5美元或90.25美元,在以上两种任一种情况下,期权到期时处于虚值状态。因此,${C_d}$的价值为零(利用对冲比率公式,在${C_{ud}} = {C_{dd}} = 0$时,对冲比率$H = 0$,${C_d} = 0$)。
最后,利用${C_u}$和${C_d}$的值求出$C$的值。该点的对冲比率为:
$H = \frac{{{C_u} – {C_d}}}{{u{S_0} – d{S_0}}} = \frac{{6.9841 – 0}}{{110 – 95}} = 0.4656$
对于每份看涨期权空头的对冲比率为买入0.4656股股票:
| $d{S_0} = 95$美元 | $u{S_0} = 110$美元 | |
| 以${S_0} = 100$美元的价格买入0.4656股股票 | 44.2326 | 51.2167 |
| 以价格$C$卖出1份看涨期权 | 0 | -6.9841 |
| 总计 | 44.2326 | 44.2326 |
该组合的当前市场价值必定等于44.2326美元的现值:
$0.4656 \times 100 – C = 44.2326/1.05 = 42.1263$
由上式可以求得$C = 4.4337$美元。
当一年分成越来越多的时间间隔时,年末股票可能价格的范围也随之扩大。
首先,注意当间隔数量增加时,股票可能的价格也增加了。其次,注意最后事件,像${u^3}{S_0}$或${d^3}{S_0}$是很少会发生的,因为它们需要在三个子间隔内连续增加或减少。中间范围的,像${u^2}d{S_0}$能通过不止一条途径得到,任何的价格两升一降组合都将会得到${u^2}d{S_0}$。因此,中间范围的值可能性更大一些。用二项式分布可以将每个结果的概率描述出来,因此这种多时期的期权定价方法被称为二项式模型(binominal model)。
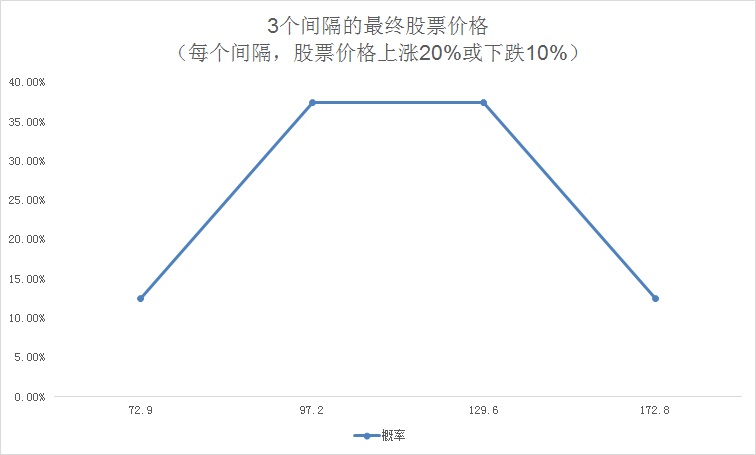
例6:初始股票价格为100美元,股票价格上涨或下跌的概率相同,三时期内股票价格可能上涨20%或下跌10%,我们能从以下的计算中得出股票价格的概率分布。三时期内股票价格的变动有八种组合:uuu、uud、udu、duu、udd、dud、ddu、ddd。每种概率都是1/8。因此,股票价格在最后一个时期期末的概率分布为:
| 事件 | 概率 | 最终股票价格 |
| 3上升 | 1/8 | $100 \times {1.2^3} = 172.8$ |
| 2升1降 | 3/8 | $100 \times {1.2^2} \times 0.9 = 129.6$ |
| 1升2降 | 3/8 | $100 \times 1.2 \times {0.9^2} = 97.2$ |
| 3下降 | 1/8 | $100 \times {0.9^3} = 72.9$ |
上例中可见,中间价值发生的概率是两端价值发生概率的3倍。频率分布如下图所示:
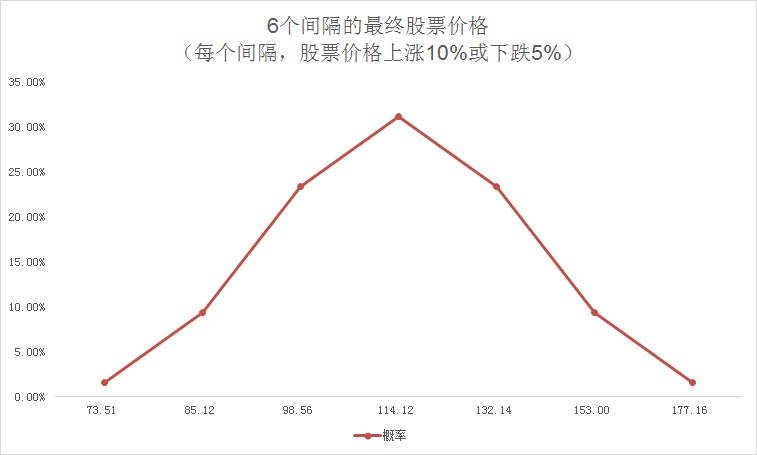
假定现在将整个持有期分成六个间隔而不是三个。因为现在设定了两倍的间隔数量,我们把股票价格可能的上涨幅度设为20%/2=10%,把可能的下跌幅度设为10%/2=5%。频率分布如下图所示:
假定现在将整个持有期分成十二个间隔。股票价格可能的上涨幅度设为5%,把可能的下跌幅度设为2.5%。频率分布如下图所示:
最后,将持有期分成越来越小的间隔,每个事件书的节点对应着无限小的时间间隔,那么在这些时间间隔内股票的变动相应的也非常小。随着时间间隔的增加,最后股票越来越接近于对数正态分布。这样,两状态模型过于简化的缺点也就可以通过时间间隔的进一步细分来克服。
在任何一个节点上,都可以构造一个在下一个时间间隔被完全对冲的资产组合。接着,在下一个时间间隔末,到达下一个节点时,又可以重新计算对冲比率,对资产组合的构成进行更新。通过不断改变对冲头寸,资产组合总可以保持在被对冲的状态,在每个时间间隔都获得无风险收益。这称为动态对冲,也就是随时间不断调整对冲比率。动态对冲越来越完善,期权的定价过程也越来越精确。
5、布莱克-斯科尔斯期权定价
尽管之前的二项式模型非常灵活,但这种方法在实际交易中需要用计算机。期权定价公式要更为简单,没有二项式模型中复杂的算法。只要做两个假设,公式就可以使用,这两个假设是无风险利率与股票价格的波动率在期权有效期内保持不变。在这种情况下,到期日前的时间被细分成更多的间隔,到期日股票价格分布渐近于对数正态分布。当股票价格分布式真正的对数分布时,我们可以得出精确的期权定价公式。
在布莱克、斯科尔斯与默顿得出看涨期权定价公式之前,金融经济学家们一直在寻找一种实用的期权定价模型。斯科尔斯与默顿因此获得了1997年诺贝尔经济学奖。现在,布莱克-斯科尔斯定价公式(Black-Scholes Pricing formula)已被期权市场参与者广泛使用。看涨期权的定价公式为:
$$C_{0}=S_{0}N\left ( d_{1} \right )-Xe^{-rT}N\left ( d_{2} \right )$$
式中:
$$d_{1}=\frac{ln\left ( S_{0}/X \right )+\left ( r+\sigma ^{2}/2 \right )T}{\sigma \sqrt{T}}$$
$$d_{2}=d_{1}-\sigma \sqrt{T}$$
$C_{0}$——当前的看涨期权价值;
$S_{0}$——当前的股票价格;
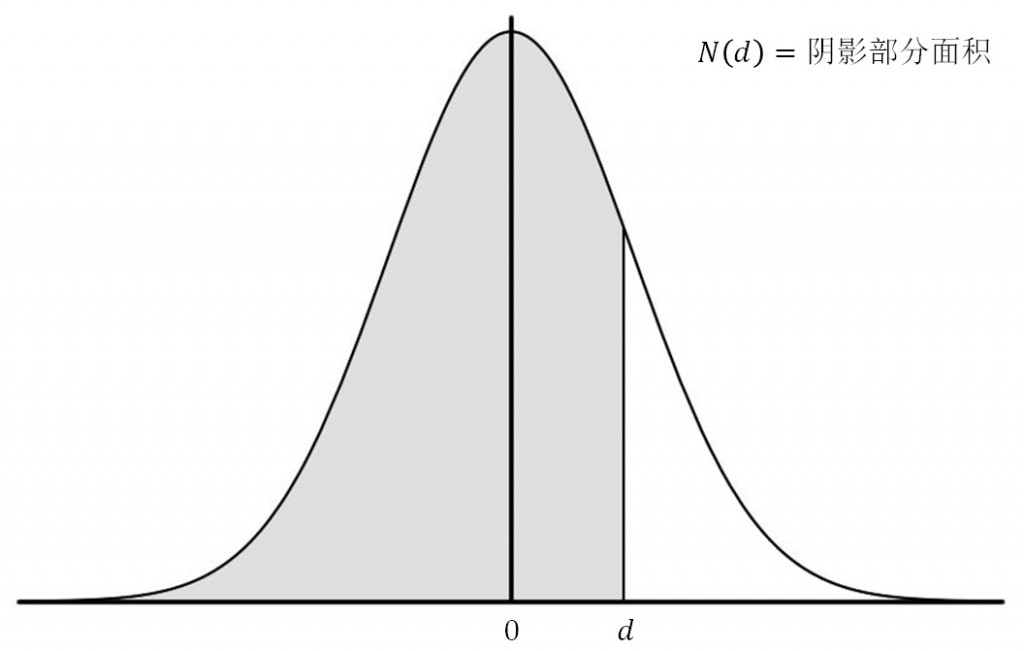
$N\left ( d \right )$——标准正态分布小于$d$的概率;
$X$——执行价格;
$e$——自然对数的底数,约为2.7183;
$r$——无风险利率;
$T$——期权到期的时间,按年记;
$ln$——自然对数函数;
$\sigma$——股票连续复利的年收益率的标准差。
由上述公式可见:期权价值并不取决于股票的期望收益率。在某种意义上说,含有股票价格的定价公式已经包括了该信息,因为股票价格取决于股票的风险与报酬特征。这里的布莱克-斯科尔斯公式假定股票不支付股利。
例7:已知条件如下:
| 股票价格 | $S_{0}=100$ | 到期期限 | $T=0.25$(3个月或一个季度) |
| 执行价格 | $X=95$ | 标准差 | $\sigma =0.50$(每年50%) |
| 利率 | $r=0.10$(每年10%) |
首先计算:
$$d_{1}=\frac{ln\left ( 100/95 \right )+\left ( 0.10+0.5^{2}/2 \right )\times 0.25}{0.5\times \sqrt{0.25}}=0.43$$
$$d_{2}=0.43-0.5\times \sqrt{0.25}=0.18$$
接下来查$N\left ( d_{1} \right )$和$N\left ( d_{2} \right )$。在很多统计学课本里可以查到正态分布表,如下表所示。任何电子数据表程序也提供正态分布函数$N\left ( d \right ) $。例如,在Excel中,程序名称为NORMSDIST。利用Excel或下表,可得到:
$$N\left ( 0.43 \right )=0.6664$$
$$N\left ( 0.18 \right )=0.5714$$
于是,看涨期权的价值为:
$$C=100\times 0.6664-95\times e^{-0.10\times 0.25}\times 0.5714=66.64-52.94=13.70$$(美元)
| 累积正态分布 | |||||||
| $d$ | $N\left ( d \right )$ | $d$ | $N\left ( d \right )$ | $d$ | $N\left ( d \right )$ | $d$ | $N\left ( d \right )$ |
| -3.00 | 0.0013 | -0.84 | 0.2005 | 0.02 | 0.5080 | 0.88 | 0.8106 |
| -2.95 | 0.0016 | -0.83 | 0.2033 | 0.03 | 0.5120 | 0.89 | 0.8133 |
| -2.90 | 0.0019 | -0.82 | 0.2061 | 0.04 | 0.5160 | 0.90 | 0.8159 |
| -2.85 | 0.0022 | -0.81 | 0.2090 | 0.05 | 0.5199 | 0.91 | 0.8186 |
| -2.80 | 0.0026 | -0.80 | 0.2119 | 0.06 | 0.5239 | 0.92 | 0.8212 |
| -2.75 | 0.0030 | -0.79 | 0.2148 | 0.07 | 0.5279 | 0.93 | 0.8238 |
| -2.70 | 0.0035 | -0.78 | 0.2177 | 0.08 | 0.5319 | 0.94 | 0.8264 |
| -2.65 | 0.0040 | -0.77 | 0.2206 | 0.09 | 0.5359 | 0.95 | 0.8289 |
| -2.60 | 0.0047 | -0.76 | 0.2236 | 0.10 | 0.5398 | 0.96 | 0.8315 |
| -2.55 | 0.0054 | -0.75 | 0.2266 | 0.11 | 0.5438 | 0.97 | 0.8340 |
| -2.50 | 0.0062 | -0.74 | 0.2296 | 0.12 | 0.5478 | 0.98 | 0.8365 |
| -2.45 | 0.0071 | -0.73 | 0.2327 | 0.13 | 0.5517 | 0.99 | 0.8389 |
| -2.40 | 0.0082 | -0.72 | 0.2358 | 0.14 | 0.5557 | 1.00 | 0.8413 |
| -2.35 | 0.0094 | -0.71 | 0.2389 | 0.15 | 0.5596 | 1.02 | 0.8461 |
| -2.30 | 0.0107 | -0.70 | 0.2420 | 0.16 | 0.5636 | 1.04 | 0.8508 |
| -2.25 | 0.0122 | -0.69 | 0.2451 | 0.17 | 0.5675 | 1.06 | 0.8554 |
| -2.20 | 0.0139 | -0.68 | 0.2483 | 0.18 | 0.5714 | 1.08 | 0.8599 |
| -2.15 | 0.0158 | -0.67 | 0.2514 | 0.19 | 0.5753 | 1.10 | 0.8643 |
| -2.10 | 0.0179 | -0.66 | 0.2546 | 0.20 | 0.5793 | 1.12 | 0.8686 |
| -2.05 | 0.0202 | -0.65 | 0.2578 | 0.21 | 0.5832 | 1.14 | 0.8729 |
| -2.00 | 0.0228 | -0.64 | 0.2611 | 0.22 | 0.5871 | 1.16 | 0.8770 |
| -1.98 | 0.0239 | -0.63 | 0.2643 | 0.23 | 0.5910 | 1.18 | 0.8810 |
| -1.96 | 0.0250 | -0.62 | 0.2676 | 0.24 | 0.5948 | 1.20 | 0.8849 |
| -1.94 | 0.0262 | -0.61 | 0.2709 | 0.25 | 0.5987 | 1.22 | 0.8888 |
| -1.92 | 0.0274 | -0.60 | 0.2743 | 0.26 | 0.6026 | 1.24 | 0.8925 |
| -1.90 | 0.0287 | -0.59 | 0.2776 | 0.27 | 0.6064 | 1.26 | 0.8962 |
| -1.88 | 0.0301 | -0.58 | 0.2810 | 0.28 | 0.6103 | 1.28 | 0.8997 |
| -1.86 | 0.0314 | -0.57 | 0.2843 | 0.29 | 0.6141 | 1.30 | 0.9032 |
| -1.84 | 0.0329 | -0.56 | 0.2877 | 0.30 | 0.6179 | 1.32 | 0.9066 |
| -1.82 | 0.0344 | -0.55 | 0.2912 | 0.31 | 0.6217 | 1.34 | 0.9099 |
| -1.80 | 0.0359 | -0.54 | 0.2946 | 0.32 | 0.6255 | 1.36 | 0.9131 |
| -1.78 | 0.0375 | -0.53 | 0.2981 | 0.33 | 0.6293 | 1.38 | 0.9162 |
| -1.76 | 0.0392 | -0.52 | 0.3015 | 0.34 | 0.6331 | 1.40 | 0.9192 |
| -1.74 | 0.0409 | -0.51 | 0.3050 | 0.35 | 0.6368 | 1.42 | 0.9222 |
| -1.72 | 0.0427 | -0.50 | 0.3085 | 0.36 | 0.6406 | 1.44 | 0.9251 |
| -1.70 | 0.0446 | -0.49 | 0.3121 | 0.37 | 0.6443 | 1.46 | 0.9279 |
| -1.68 | 0.0465 | -0.48 | 0.3156 | 0.38 | 0.6480 | 1.48 | 0.9306 |
| -1.66 | 0.0485 | -0.47 | 0.3192 | 0.39 | 0.6517 | 1.50 | 0.9332 |
| -1.64 | 0.0505 | -0.46 | 0.3228 | 0.40 | 0.6554 | 1.52 | 0.9357 |
| -1.62 | 0.0526 | -0.45 | 0.3264 | 0.41 | 0.6591 | 1.54 | 0.9382 |
| -1.60 | 0.0548 | -0.44 | 0.3300 | 0.42 | 0.6628 | 1.56 | 0.9406 |
| -1.58 | 0.0571 | -0.43 | 0.3336 | 0.43 | 0.6664 | 1.58 | 0.9429 |
| -1.56 | 0.0594 | -0.42 | 0.3372 | 0.44 | 0.6700 | 1.60 | 0.9452 |
| -1.54 | 0.0618 | -0.41 | 0.3409 | 0.45 | 0.6736 | 1.62 | 0.9474 |
| -1.52 | 0.0643 | -0.40 | 0.3446 | 0.46 | 0.6772 | 1.64 | 0.9495 |
| -1.50 | 0.0668 | -0.39 | 0.3483 | 0.47 | 0.6808 | 1.66 | 0.9515 |
| -1.48 | 0.0694 | -0.38 | 0.3520 | 0.48 | 0.6844 | 1.68 | 0.9535 |
| -1.46 | 0.0721 | -0.37 | 0.3557 | 0.49 | 0.6879 | 1.70 | 0.9554 |
| -1.44 | 0.0749 | -0.36 | 0.3594 | 0.50 | 0.6915 | 1.72 | 0.9573 |
| -1.42 | 0.0778 | -0.35 | 0.3632 | 0.51 | 0.6950 | 1.74 | 0.9591 |
| -1.40 | 0.0808 | -0.34 | 0.3669 | 0.52 | 0.6985 | 1.76 | 0.9608 |
| -1.38 | 0.0838 | -0.33 | 0.3707 | 0.53 | 0.7019 | 1.78 | 0.9625 |
| -1.36 | 0.0869 | -0.32 | 0.3745 | 0.54 | 0.7054 | 1.80 | 0.9641 |
| -1.34 | 0.0901 | -0.31 | 0.3783 | 0.55 | 0.7088 | 1.82 | 0.9656 |
| -1.32 | 0.0934 | -0.30 | 0.3821 | 0.56 | 0.7123 | 1.84 | 0.9671 |
| -1.30 | 0.0968 | -0.29 | 0.3859 | 0.57 | 0.7157 | 1.86 | 0.9686 |
| -1.28 | 0.1003 | -0.28 | 0.3897 | 0.58 | 0.7190 | 1.88 | 0.9699 |
| -1.26 | 0.1038 | -0.27 | 0.3936 | 0.59 | 0.7224 | 1.90 | 0.9713 |
| -1.24 | 0.1075 | -0.26 | 0.3974 | 0.60 | 0.7257 | 1.92 | 0.9726 |
| -1.22 | 0.1112 | -0.25 | 0.4013 | 0.61 | 0.7291 | 1.94 | 0.9738 |
| -1.20 | 0.1151 | -0.24 | 0.4052 | 0.62 | 0.7324 | 1.96 | 0.9750 |
| -1.18 | 0.1190 | -0.23 | 0.4090 | 0.63 | 0.7357 | 1.98 | 0.9761 |
| -1.16 | 0.1230 | -0.22 | 0.4129 | 0.64 | 0.7389 | 2.00 | 0.9772 |
| -1.14 | 0.1271 | -0.21 | 0.4168 | 0.65 | 0.7422 | 2.05 | 0.9798 |
| -1.12 | 0.1314 | -0.20 | 0.4207 | 0.66 | 0.7454 | 2.10 | 0.9821 |
| -1.10 | 0.1357 | -0.19 | 0.4247 | 0.67 | 0.7486 | 2.15 | 0.9842 |
| -1.08 | 0.1401 | -0.18 | 0.4286 | 0.68 | 0.7517 | 2.20 | 0.9861 |
| -1.06 | 0.1446 | -0.17 | 0.4325 | 0.69 | 0.7549 | 2.25 | 0.9878 |
| -1.04 | 0.1492 | -0.16 | 0.4364 | 0.70 | 0.7580 | 2.30 | 0.9893 |
| -1.02 | 0.1539 | -0.15 | 0.4404 | 0.71 | 0.7611 | 2.35 | 0.9906 |
| -1.00 | 0.1587 | -0.14 | 0.4443 | 0.72 | 0.7642 | 2.40 | 0.9918 |
| -0.99 | 0.1611 | -0.13 | 0.4483 | 0.73 | 0.7673 | 2.45 | 0.9929 |
| -0.98 | 0.1635 | -0.12 | 0.4522 | 0.74 | 0.7704 | 2.50 | 0.9938 |
| -0.97 | 0.1660 | -0.11 | 0.4562 | 0.75 | 0.7734 | 2.55 | 0.9946 |
| -0.96 | 0.1685 | -0.10 | 0.4602 | 0.76 | 0.7764 | 2.60 | 0.9953 |
| -0.95 | 0.1711 | -0.09 | 0.4641 | 0.77 | 0.7794 | 2.65 | 0.9960 |
| -0.94 | 0.1736 | -0.08 | 0.4681 | 0.78 | 0.7823 | 2.70 | 0.9965 |
| -0.93 | 0.1762 | -0.07 | 0.4721 | 0.79 | 0.7852 | 2.75 | 0.9970 |
| -0.92 | 0.1788 | -0.06 | 0.4761 | 0.80 | 0.7881 | 2.80 | 0.9974 |
| -0.91 | 0.1814 | -0.05 | 0.4801 | 0.81 | 0.7910 | 2.85 | 0.9978 |
| -0.90 | 0.1841 | -0.04 | 0.4840 | 0.82 | 0.7939 | 2.90 | 0.9981 |
| -0.89 | 0.1867 | -0.03 | 0.4880 | 0.83 | 0.7967 | 2.95 | 0.9984 |
| -0.88 | 0.1894 | -0.02 | 0.4920 | 0.84 | 0.7995 | 3.00 | 0.9987 |
| -0.87 | 0.1922 | -0.01 | 0.4960 | 0.85 | 0.8023 | ||
| -0.86 | 0.1949 | 0.00 | 0.5000 | 0.86 | 0.8051 | ||
| -0.85 | 0.1977 | 0.01 | 0.5040 | 0.87 | 0.8078 | ||
首先,同所有模型一项,布莱克-斯科尔斯公式也是建立在是该模型近似有效的抽象简化基础之上。
公式的一些重要假设如下:
(1)在期权到期日之前,股票不支付股利;
(2)利率$r$与股票的方差$\sigma ^{2}$保持不变(或者更一般化的,两者都是时间的已知函数,任何变化都可预测);
(3)股票价格是连续的,也就是说股票价格不会发生异常的波动,比如公司被接管声明导致的价格异常波动。
如今,已有变形的布莱克-斯科尔斯公式来处理以上的这些限制条件。
其次,在布莱克-斯科尔斯模型中,必须保证公式中各个参数是正确的。其中的四个值($S_{0}$、$X$、$T$和$r$)都是很直接的。股票价格、执行价格和到期期限都是给定的。利率是相同期限的货币市场利率,并且股利支付至少在短期内是可以合理预测的。
最后一个输入变量是股票收益率的方差,不能直接观察到。必须从历史数据、情境分析或者其他期权价格中估计出来,所以真实的期权价格与用公式算出的期权价格有可能不同,这是由股票的波动率估计误差造成的。
事实上,市场参与者往往从不同的角度来看期权定价问题。一般不是用所给的股票标准差按布莱克-斯科尔斯公式计算期权价格,而是会问:如果观察到的期权价格与布莱克-斯科尔斯公式计算出来的期权价格一致的话,那么标准差是多少呢?这就使期权的隐含波动率(implied volatility),即期权价格中隐含的股票波动率水平。投资者可以判断实际的股票标准差是否超过了隐含波动率。如果超过了,则购买期权是一个好的选择;如果实际波动率高于隐含波动率,期权的公允价格就要高于观察到的价格。
另一个角度是比较到期日相同、执行价格不同的同一股票的期权。具有较高隐含波动率的期权相对贵一些,因为需要较高的标准差来调节价格。
布莱克-斯科尔斯定价公式,以及隐含波动率,很容易使用Excel中的电子数据表进行计算,如下表所示。模型的输入部分在C2~C7,输出部分在B9~B14,C9~C14还给出了输出部分的计算公式。
| A | B | C | |
| 1 | INPUTS | ||
| 2 | 标准差Standard deviation(annual) | $\sigma$ | 0.2783 |
| 3 | 到期期限Maturity(in years) | $T$ | 0.5 |
| 4 | 年化无风险利率Risk-free rate(annual) | $r$ | 0.06 |
| 5 | 股票价格Stock price | $S_{0}$ | 100 |
| 6 | 执行价格Exercise price | $X$ | 105 |
| 7 | 年化股息收益率Dividend yield(annual) | $\delta$ | 0 |
| 8 | OUTPUTS | FORMULA FOR OUTPUT IN COLUMN B9 to B14 | |
| 9 | d1 | 0.0029 | (LN(C5/C6)+(C4-C7+0.5*C2^2)*C3)/(C2*SQRT(C3)) |
| 10 | d2 | -0.1939 | B9-C2*SQRT(C3) |
| 11 | N(d1) | 0.5012 | NORMSDIST(B9) |
| 12 | N(d2) | 0.4231 | NORMSDIST(B10) |
| 13 | 看涨期权价值B/S call vallue,&C_{0}$ | 6.9999 | C5*EXP(-C7*C3)*B11-C6*EXP(-C4*C3)*B12 |
| 14 | 看跌期权价值B/S put vallue,&P_{0}$ | 8.8967 | C6*EXP(-C4*C3)*(1-B12)-C5*EXP(-C7*C3)*(1-B11) |
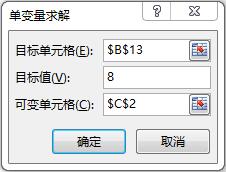
如需计算隐含波动率,可以使用Excel菜单中的“数据”→“模拟分析”→“单变量求解”命令(Excel2013),如下图所示。该命令可以通过改变一个单元格的值以使另一个单元格的值等于一个特定的值。例如,输入部分如上表所示,当看涨期权B13单元格的值等于8时,可变单元格C2会计算出相应值。
6、股利与看涨期权定价
布莱克-斯科尔斯公式要求股票不支付股利,当在期权到期之前股票支付股利时,就要调整公式。股利的支付,提高了提前执行期权的可能性,对更接近现实支付股利的情况,定价公式变得比布莱克-斯科尔斯公式更为复杂。
假定期权持有至到期,则期权价值的计算方法与之前相同。假定标的资产支付连续现金收入。如果股利率保持不变,记为$\delta$到期之前累计股利的现值为$S_{0}\left ( 1-e^{-\delta T} \right )$。将该红利从当前股票价格$S_{0}$中减去,得:$S_{0}e^{-\delta T}$。将其带入布莱克-斯科尔斯看涨期权公式,即可得到:$$C_{0}=S_{0}e^{-\delta T}N\left ( d_{1} \right )-Xe^{-rT}N\left ( d_{2} \right )$$
7、看跌期权定价
通过看跌-看涨期权平价定理得到布莱克-斯科尔斯欧式看跌期权定价公式:
$$P=C+Xe^{-rT}-S_{0}$$
如果将看涨布莱克-斯科尔斯定价公式直接代入上式,可以得到看跌期权价值为:
$$P _{0}=Xe^{-rT}\left [ 1-N\left ( d_{2} \right ) \right ]-S_{0}\left [ 1-N\left ( d_{1} \right ) \right ]$$
8、股利与看跌期权定价
将$S_{0}e^{-\delta T}$代入布莱克-斯科尔斯看跌期权公式,可得:$$P_{0}=Xe^{-rT}\left [ 1-N\left ( d_{2} \right ) \right ]-S_{0}e^{-\delta T}\left [ 1-N\left ( d_{1} \right ) \right ]$$