互换定价
互换(Swap)是指交易双方同意在约定的时间长度内,按照制定货币以约定形式交换一系列现金流支付的行为。常见的互换有利率互换、货币互换和权益互换等。
一、利率互换(Interest Rate Swap)
利率互换是指两笔货币相同、债务额相同(本金相同)、期限相同的资金,作固定利率(fixed interest rate)与浮动利率(floating interest rate)的调换。这个调换是双方的,如甲方以固定利率换取乙方的浮动利率,乙方则以浮动利率换取甲方的固定利率,故称互换。互换的目的在于降低资金成本和利率风险。
利率互换交易的基本原理就是比较优势理论与利益共享。首先,根据比较优势理论,由于筹资双方信用等级、筹资渠道、地理位置以及信息掌握程度等方面的不同,在各自的领域存在着比较优势。因此,双方愿意达成协议,发挥各自优势,然后再互相交换债务,达到两者总成本的降低,进而由于利益共享,最终使得互换双方的筹资成本都能够得到一定的降低。
例如甲国和乙国都只生产衣服和食物,在同质的资源下,甲国生产一单位衣服的机会成本是二单位食物,而乙国生产一单位衣服的机会成本是三单位食物,根据比较优势理论,甲国享有生产衣服的比较优势,便应该专业生产衣服,并出口之,以换取食物。而乙国在生产衣服上有比较劣势,意味它生产食物享有比较优势。没有任何一方在所有物品的生产上均享有比较优势,所以比较优势的本质是互利的。
例1:假设有甲、乙两家公司,都想借入5年期的1000万美元借款,其信用等级及各自在固定利率市场和浮动利率市场上的借款成本如下表所示:
| 甲公司 | 乙公司 | |
| 信用等级 | AAA | BBB |
| 固定利率 | 9% | 10.5% |
| 浮动利率 | 6个月LIBOR+0.2% | 6个月LIBOR+0.5% |
通过表中的数据可以看出,甲公司由于信用等级高,在固定利率市场和浮动利率市场都有优势。两公司固定利率之差为1.5%,而浮动利率之差为0.3%。因此,甲公司在固定利率市场具有比较优势,而乙公司在浮动利率市场具有比较优势。
假设甲公司希望支付浮动利率利息,乙公司希望支付固定利率利息,如果二者按照各自原本的借款成本借款,甲公司的利率为:6个月LIBOR+0.2%,乙公司的利率为10.5%,总的成本为:6个月LIBOR+0.2%+10.5%=6个月LIBOR+10.7%。
根据双方的比较优势,甲公司借入固定利率贷款,乙公司借入浮动利率贷款,然后再进行互换,总的成本为:9%+6个月LIBOR+0.5%=6个月LIBOR+9.5%。
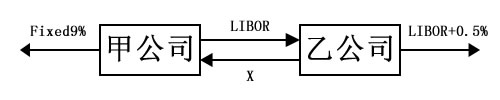
相对于不进行互换而言一共节省成本1.2%。双方可以按照事先确定的比例分享这部分节省下来的成本。假设甲乙公司利益均分,即每一方节省0.6%,甲方互换后利率为:6个月LIBOR+0.2%-0.6%=6个月LIBOR-0.4%;乙方互换后利率为:10.5%-0.6%=9.9%。具体的操作流程可以由下图演示:
甲公司的现金流:(1)支付给外部贷款方的9%固定利率利息;(2)支付给乙公司的六个月LIBOR浮动利率利息;(3)从乙公司得到的X固定利率利息。-9%-6个月LIBOR+X=-(6个月LIBOR-0.4%),得:X=9.4%;
乙公司的现金流:(1)支付给外部贷款方的六个月LIBOR+0.5%浮动利率利息;(2)从甲公司得到的六个月LIBOR浮动利率利息;(3)支付给甲公司的X固定利率利息。-(6个月LIBOR+0.5%)-X+6个月LIBOR=-9.9%,得:X=9.4%。
在上述互换中,每隔6个月为利息支付日,因此互换协议的条款应规定每6个月一方向另一方支付固定利率与浮动利率的差额。假定某一支付日的LIBOR为8.7%,乙公司需支付3.5万美元(即1000万*(9.4%-8.7%)*0.5)给甲公司。
利率互换合约可以看作面值等额的固定利率债券和浮动利率债券之间的交换,上例中甲、乙两公司的利率互换,可以分解为,乙公司按6个月LIBOR的利率借给甲公司1000万美元,甲公司按9.4%的年利率借给乙公司1000万美元。换个角度看,就是:
(1)甲公司向乙公司购买了一份1000万美元的固定利率债券;
(2)乙公司向甲公司购买了一份1000万美元的浮动利率债券。
固定利率支付者(乙公司):在利率互换交易中支付固定利率,接受浮动利率,买进互换,是互换交易多头;是债券市场空头。
浮动利率支付者(甲公司):在利率互换交易中支付浮动利率,接受固定利率,卖出互换,是互换交易空头;是债券市场多头。
签订之初,固定利率债券和浮动利率债券的价值相等,互换合约的价值为零。但是随着时间的推移,利率期限结构会发生变化,两份债券的价值不在相等,因此互换合约价值${V_{swap}}$也将不再为零。
对于支付固定利率的一方,合约价值为浮动利率债券价值${B_{fl}}$减去固定利率债券价值${B_{fix}}$:$${V_{swap}} = {B_{fl}} – {B_{fix}}$$
对于支付浮动利率的一方,合约价值为固定利率债券价值${B_{fix}}$减去浮动利率债券价值${B_{fl}}$:$${V_{swap}} = {B_{fix}} – {B_{fl}}$$
利率互换中固定利率的一般公式为:
$${R_{fix}} = \left( {\frac{{1 – {D_n}}}{{{D_1} + {D_2} + \cdot \cdot \cdot + {D_i} + \cdot \cdot \cdot + {D_n}}}} \right) \times m$$
式中,${{D_i}}$表示第$i$次互换时的折现因子,$n$表示互换的总次数,$m$表示每年互换的次数。
(1)折现因子:表示当年利率为$r$,每年复利一次,$T$时期之后1美元的现值,即$\frac{1}{{{{\left( {1 + r} \right)}^T}}}$,被称为未来T时期的货币的折现因子(discount factor)。
单利折现因子:$\frac{1}{{1 + r \times T}}$
复利折现因子:$\frac{1}{{{{\left( {1 + r} \right)}^T}}}$
连续复利折现因子:${e^{ – r \times T}}$
(2)零息债券定价,不支付利息,到期日一次性还本付息的债券,这种债券的定价公式最简单,债券的价值${P_v}$可用下式确定:$${P_v} = \frac{F}{{{{\left( {1 + r} \right)}^T}}}$$
${P_v}$为债券当前市场价格;
${F}$为债券面值(face Value);
${r}$为到期收益率(Yield To Maturity,YTM);
${T}$为待偿期,债券到期支付剩余年限;
(3)付息债券定价,设债券每年一次性支付利息${C}$(元),则债券的价值${P_v}$为:$${P_v} = \sum\limits_{t = 1}^T {\frac{C}{{{{\left( {1 + r} \right)}^t}}}} + \frac{F}{{{{\left( {1 + r} \right)}^T}}}$$
${C}$为按票面利率每年支付的利息(coupon rate);
(4)每年派息${m}$次的债券,如果每年支付的利息${C}$按${m}$次支付,则此债券的价格为:$${P_v} = \sum\limits_{t = 1}^{mT} {\frac{{C/m}}{{{{\left( {1 + {r_t}/m} \right)}^t}}}} + \frac{F}{{{{\left( {1 + {r_t}/m} \right)}^{mT}}}}$$
(5)当$m \to \infty $时,债券定价为:
$${P_v} = \sum\limits_{i = 1}^n {C \cdot {e^{ – {r_i}{t_i}}}} + F \cdot {e^{ – {r_n}{t_n}}}$$
若固定利率未知,假定债券面值${F^ * }$为1元,则固定利率债券价值初值$B_{fix}^ * $亦为1元:
$B_{fix}^ * = \frac{C}{m} \cdot \left( {\frac{1}{{1 + {r_1}}} + \frac{1}{{1 + {r_2}}} + \cdot \cdot \cdot + \frac{1}{{1 + {r_i}}} + \cdot \cdot \cdot + \frac{1}{{1 + {r_n}}}} \right) + {F^ * } \cdot \frac{1}{{1 + {r_n}}}$
$B_{fix}^ * = \frac{C}{m} \cdot \left( {{D_1} + {D_2} + \cdot \cdot \cdot + {D_i} + \cdot \cdot \cdot + {D_n}} \right) + {F^ * } \cdot {D_n}$
$ \Rightarrow C = \frac{{\left( {B_{fix}^* – {F^*} \cdot {D_n}} \right) \cdot m}}{{{D_1} + {D_2} + \cdot \cdot \cdot + {D_i} + \cdot \cdot \cdot + {D_n}}}$
式中,按票面利率每年支付的利息${C}$,即为利率互换中的固定利率${R_{fix}}$。
例2:某利率互换期限为一年,每半年互换一次,假设名义本金为2500万美元。Libor当前的利率期限结构表如下所示。计算互换的固定利率。
| 期限 | 即期利率 | 折现因子换算 | 折现因子 |
| 180天 | 5.85% | 1/(1+5.85%*180/360) | 0.9716 |
| 360天 | 6.05% | 1/(1+6.05%*360/360) | 0.9430 |
| 540天 | 6.24% | 1/(1+6.24%*540/360) | 0.9144 |
| 720天 | 6.65% | 1/(1+6.65%*720/360) | 0.8826 |
${R_{fix}} = \frac{{1 – 0.8826}}{{0.9716 + 0.9430 + 0.9144 + 0.8826}} \times 2 = 0.0633$
假设当前时刻为${t_1}$,下一次支付利息的时刻为${t_2}$,浮动支付为$c$。已知浮动利率债券每次支付利息后的价值等于其面值$F$,则其在下一个支付日${t_2}$付息前的价值应为$\left( {F + c} \right)$。我们只需要利用对应的折现因子${D_{{t_2} – {t_1}}}$,将$\left( {F + c} \right)$从${t_2}$时刻折现到${t_1}$时刻,即可得到浮动利率债券的价值${B_{fl}}$。
$${B_{fl}} = \left( {F + c} \right){D_{{t_2} – {t_1}}}$$
固定利率债券的价值${B_{fix}}$计算方式也比较简单,只需要用新的对应期限的折现因子对未来收到的利息和本金现金流进行贴现即可。
例3:接上例,120天后新的利率期限结构表如下所示。计算对于浮动利率支付方,互换合约的价值是多少?
| 期限 | 即期利率 | 折现因子换算 | 折现因子 |
| 60天 | 6.13% | 1/(1+6.13%*60/360) | 0.9899 |
| 240天 | 6.29% | 1/(1+6.29%*240/360) | 0.9598 |
| 420天 | 6.53% | 1/(1+6.53%*420/360) | 0.9292 |
| 600天 | 6.97% | 1/(1+6.97%*600/360) | 0.8959 |
首先,计算固定利率债券价格。假设名义本金${F^ * }$为1美元,120天后固定利率债券的价格为:
$B_{fix}^ * = C \cdot \left( {{D_1} + {D_2} + \cdot \cdot \cdot + {D_i} + \cdot \cdot \cdot + {D_n}} \right) + {F^ * } \cdot {D_n}$
$B_{fix}^ * = 0.0317 \times \left( {0.9899 + 0.9598 + 0.9292 + 0.8959} \right) + 1 \times 0.8959$
$B_{fix}^ * = 1.0156$(美元)
其次,计算浮动利率债券价格。假设名义本金${F^ * }$为1美元,首次互换的浮动利率债券支付为:
${c^ * } = {F^ * } \cdot {r_1} \cdot {t_1} = 1 \times 5.85\% \times \left( {180/360} \right) = 0.0293$
那么浮动利率债券的价格为:
$B_{fl}^* = \left( {{F^*} + {c^*}} \right) \cdot {D_1}$
$B_{fl}^* = \left( {1 + 0.0293} \right) \times 0.9899$
$B_{fl}^* = 1.0188$(美元)
最后,由于互换名义本金$F$为2500万美元,对于浮动利率支付方,该互换合约的价值为:
${V_{swap}} = {B_{fix}} – {B_{fl}}$
${V_{swap}} = F \cdot B_{fix}^* – F \cdot B_{fl}^*$
${V_{swap}} = 2500 \times \left( {1.0156 – 1.0188} \right)$
${V_{swap}} = – 8$(万美元)
二、货币互换(Currency Swap)
货币互换是指两笔金额相同、期限相同、计算利率方法相同,但货币不同的债务资金之间的调换,同时也进行不同利息额的货币调换。简单来说,利率互换是相同货币债务间的调换,而货币互换则是不同货币债务间的调换。
货币互换的主要原因是双方在各自国家中的金融市场上具有比较优势。
例4:假设有甲、乙两甲公司,当前汇率为1.4USD/GBP,甲公司想借入5年期的1000万英镑借款,乙公司想借入5年期的1400万美元借款。市场向他们提供的固定利率借款成本如下表所示:
| 甲公司 | 乙公司 | |
| 固定利率(美元) | 8% | 10% |
| 固定利率(英镑) | 11.6% | 12% |
通过表中的数据可以看出,甲公司在美元和英镑市场上的借款成本都有优势,美元市场上的固定利率之差为2%,而英镑市场上的固定利率之差为0.4%。因此,甲公司在美元市场上的固定利率具有比较优势,而乙公司在英镑市场上的固定利率具有比较优势。
如果二者按照各自原有的借款成本借款,甲公司的利率为11.6%,乙公司的利率为10%,总的成本为:11.6%+10%=21.6%。
根据双方的比较优势,甲公司借入美元,乙公司借入英镑,然后进行互换,总的成本为:8%+12%=20%。
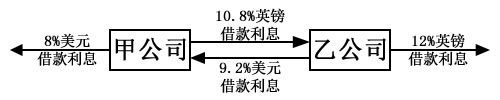
相对于不进行互换而言一共节省成本1.6%。双方可以按照事先确定的比例分享这部分节省下来的成本。假设甲乙公司利益均分,即每一方节省0.8%,甲方互换后利率为:11.6%-0.8%=10.8%;一方互换后利率为:10%-0.8%=9.2%。具体的操作流程可以由下图演示:
甲公司的现金流:(1)支付给外部贷款方的8%美元利息(1400万美元*8%=112万美元);(2)支付给乙公司的10.8%英镑利息(1000万英镑*10.8%=108万英镑,折合成151.2万美元);(3)从乙公司得到的9.2%美元利息(1400万美元*9.2%=128.8万美元)。总计:-112-151.2+128.8=-134.4(万美元),即9.6%美元固定利率利息。
乙公司的现金流:(1)支付给外部贷款方的12%英镑利息(1000万英镑*12%=120万英镑);(2)支付给甲公司的9.2%美元利息(1400万美元*9.2%=128.8万美元,折合成92万英镑);(3)从甲公司得到的10.8%英镑利息(1000万美元*10.8%=108万英镑)。总计:-120-92+108=-104(万英镑),折合成-145.6(万美元),即10.4%英镑固定利率利息。
货币互换合约可以看作是不同币种债券的组合,然后加上一个外汇市场交易。上例中,甲公司持有的互换头寸可以看作是一份年利率为9.2%的美元债券多头头寸和一份年利率为10.8%的英镑债券空头头寸的组合;乙公司持有的互换头寸可以看作是一份年利率为9.2%的美元债券空头头寸和一份年利率为10.8%的英镑债券多头头寸的组合。
货币互换合约签订之初,美元债券和英镑债券的价值相等,随着时间的推移,各国的利率期限结构发生了变化,即期汇率也发生了变化,两张债券的价值就不相等了。
以本币和外币的货币互换为例,对于本币支付方,其互换价值为外币债券价值减去本币债券价值(以本币标价):
$${V_{swap}} = S{B_f} – {B_d}$$
对于外币支付方,其互换价值为本币债券价值减去外币债券价值(以外币标价):
$${V_{swap}} = {B_d}/S – {B_f}$$
其中,即期汇率$S$采用直接标价法。两个债券价值${B_d}$和${B_f}$的计算方法与利率互换中介绍的方法相同,利用两个国家不同的利率期限结构分别计算得出。
货币互换中的固定利率价公式为:
$${R_{fix}} = \left( {\frac{{1 – {D_n}}}{{{D_1} + {D_2} + \cdot \cdot \cdot + {D_i} + \cdot \cdot \cdot + {D_n}}}} \right) \cdot m$$
例5:某期限为2年的货币互换合约,每半年互换一次。假设本国使用货币为美元,外国使用货币为英镑,当前汇率${S_1}$为1.4USD/GBP。
(1)当前美国和英国的利率期限结构如下表所示:
| 期限 | 即期利率U.S. | 折现因子U.S. | 即期利率U.K. | 折现因子U.K. |
| 180天 | 5.85% | 0.9716 | 4.93% | 0.9759 |
| 360天 | 6.05% | 0.9430 | 5.05% | 0.9519 |
| 540天 | 6.24% | 0.9144 | 5.19% | 0.9278 |
| 720天 | 6.65% | 0.8826 | 5.51% | 0.9007 |
分别计算互换中美元与英镑的固定利率。
假设名义本金$F_{USD}^ * $为1美元,则美元固定利率为:
${R_{d}} = \frac{{1 – 0.8826}}{{0.9716 + 0.9430 + 0.9144 + 0.8826}} \times 2 = 0.0633$
假设名义本金$F_{GBP}^ * $为1英镑,则英镑固定利率为:
${R_{f}} = \frac{{1 – 0.9007}}{{0.9759 + 0.9519 + 0.9278 + 0.9007}} \times 2 = 0.0529$
(2)120天后,即期汇率${S_2}$为1.35USD/GBP,新的利率期限结构如下表所示:
| 期限 | 即期利率U.S. | 折现因子U.S. | 即期利率U.K. | 折现因子U.K. |
| 60天 | 6.13% | 0.9899 | 5.17% | 0.9915 |
| 240天 | 6.29% | 0.9598 | 5.32% | 0.9657 |
| 420天 | 6.53% | 0.9292 | 5.68% | 0.9379 |
| 600天 | 6.97% | 0.8959 | 5.83% | 0.9114 |
假设名义本金为1美元,计算支付英镑固定利率交换美元固定利率的互换合约的价值。
首先,计算美元固定利率债券价格。名义本金${F_{USD}}$为1美元,120天后固定利率债券的价格为:
${B_d} = {C_{USD}} \cdot \left( {{D_1} + {D_2} + \cdot \cdot \cdot + {D_i} + \cdot \cdot \cdot + {D_n}} \right) + {F_{USD}} \cdot {D_n}$
${B_d} = 0.0317 \times \left( {0.9899 + 0.9598 + 0.9292 + 0.8959} \right) + 1 \times 0.8959$
${B_d} = 1.0156$(美元)。
其次,计算英镑固定利率债券价格。按照初期利率${S_1}$为1.4USD/GBP换算,名义本金${F_{GBP}}$为1/1.4英镑,120天后固定利率债券的价格为:
${B_f} = {C_{GBP}} \cdot \left( {{D_1} + {D_2} + \cdot \cdot \cdot + {D_i} + \cdot \cdot \cdot + {D_n}} \right) + {F_{GBP}} \cdot {D_n}$
${B_f} = \left( {1/1.4} \right) \times 0.0265 \times \left( {0.9915 + 0.9657 + 0.9379 + 0.9114} \right) + \left( {1/1.4} \right) \times 0.9114$
${B_f} = 0.7231$(英镑)
将此价格按照即期汇率${S_2}$为1.35USD/GBP,换算成为美元计价:
${B_f} = 1.35 \times 0.7231 = 0.9762$(美元)
支付英镑固定利率交换美元固定利率的互换合约价值为:
${V_{swap}} = 1.0156 – 0.9762 = 0.0394$(美元)
参考(1):
假设名义本金为1美元,计算支付美元固定利率交换英镑固定利率的互换合约的价值。
首先,计算美元固定利率债券价格。名义本金${F_{USD}}$为1美元,120天后固定利率债券的价格为:
${B_d} = {C_{USD}} \cdot \left( {{D_1} + {D_2} + \cdot \cdot \cdot + {D_i} + \cdot \cdot \cdot + {D_n}} \right) + {F_{USD}} \cdot {D_n}$
${B_d} = 0.0317 \times \left( {0.9899 + 0.9598 + 0.9292 + 0.8959} \right) + 1 \times 0.8959$
${B_d} = 1.0156$(美元)。
其次,计算英镑固定利率债券价格。按照初期利率${S_1}$为1.4USD/GBP换算,名义本金${F_{GBP}}$为1/1.4英镑,120天后固定利率债券的价格为:
${B_f} = {C_{GBP}} \cdot \left( {{D_1} + {D_2} + \cdot \cdot \cdot + {D_i} + \cdot \cdot \cdot + {D_n}} \right) + {F_{GBP}} \cdot {D_n}$
${B_f} = \left( {1/1.4} \right) \times 0.0265 \times \left( {0.9915 + 0.9657 + 0.9379 + 0.9114} \right) + \left( {1/1.4} \right) \times 0.9114$
${B_f} = 0.7231$(英镑)
120天后,即期汇率${S_2}$为1.35USD/GBP,支付美元固定利率交换英镑固定利率的互换合约价值为:
${V_{swap}} = {S_2}{B_f} – {B_d}$
${V_{swap}} = 1.35 \times 0.7231 – 1.0516$
${V_{swap}} = -0.0394$(美元)
参考(2):
假设名义本金为1英镑,计算支付英镑固定利率交换美元固定利率的互换合约的价值。
首先,计算英镑固定利率债券价格。名义本金${F_{GBP}}$为1英镑,120天后固定利率债券的价格为:
${B_d} = {C_{GBP}} \cdot \left( {{D_1} + {D_2} + \cdot \cdot \cdot + {D_i} + \cdot \cdot \cdot + {D_n}} \right) + {F_{GBP}} \cdot {D_n}$
${B_f} = 0.0265 \times \left( {0.9915 + 0.9657 + 0.9379 + 0.9114} \right) + 1 \times 0.9114$
${B_d} = 1.0123$(英镑)。
其次,计算美元固定利率债券价格。按照初期利率${S_1}$为1.4USD/GBP换算,名义本金${F_{USD}}$为1.4美元,120天后固定利率债券的价格为:
${B_f} = {C_{USD}} \cdot \left( {{D_1} + {D_2} + \cdot \cdot \cdot + {D_i} + \cdot \cdot \cdot + {D_n}} \right) + {F_{USD}} \cdot {D_n}$
${B_f} = 1.4 \times 0.0317 \times \left( {0.9899 + 0.9598 + 0.9292 + 0.8959} \right) + 1.4 \times 0.8959$
${B_f} = 1.4218$(美元)
120天后,即期汇率${S_2}$为1.35USD/GBP,支付英镑固定利率交换美元固定利率的互换合约价值为:
${V_{swap}} = {B_d}/{S_2} – {B_f}$
${V_{swap}} = 1.4218/1.35 – 1.0123$
${V_{swap}} = 0.0409$(英镑)
三、权益互换(Equity Swap)
权益互换,是指投资者与券商或投资机构根据协议约定,在未来一段期限内,针对特定股票或指数的收益表现,与固定利率进行现金流交换,是一种重要的权益衍生工具交易形式。
权益互换合约签订之后,随着时间的推移,利率期限结构发生了变化,权益政权的价格也发生了变化,两张证券的价值不在相等。
对于权益收益率支付方,权益互换合约价值为:
$${V_{swap}} = {B_{fix}} – {V_{equity}}$$
对于固定利率支付方,权益互换合约价值为:
$${V_{swap}} = {V_{equity}} – {B_{fix}}$$
权益政权的价值${V_{equity}}$计算公式为:
$${V_{equity}} = \frac{P}{{{P_{\left[ 1 \right]}}}} \cdot F$$
$P$为当前权益证券的价格;
${{P_{\left[ 1 \right]}}}$为上一次的权益证券的价格;
$P$为名义本金;
权益互换中的固定利率的公式为:
$${R_{fix}} = \left( {\frac{{1 – {D_n}}}{{{D_1} + {D_2} + \cdot \cdot \cdot + {D_i} + \cdot \cdot \cdot + {D_n}}}} \right) \cdot m$$
例6:某投资者与投资银行签订了一个为期2年的股权互换,名义本金为100万美元,每半年互换一次。在此互换中,他将支付固定利率以换取标普500指数的收益率。合约签订之初,标普500指数为1150.89点,当前利率期限结构如下表所示:
| 期限 | 即期利率 | 折现因子 |
| 180天 | 4.58% | 0.9776 |
| 360天 | 5.28% | 0.9498 |
| 540天 | 6.24% | 0.9144 |
| 720天 | 6.65% | 0.8826 |
(1)计算该投资者支付的固定利率。
假设名义本金${F^ * }$为1美元,则固定利率为:
${R_{fix}} = \frac{{1 – 0.8826}}{{0.9776 + 0.9498 + 0.9144 + 0.8826}} \times 2 = 0.0630$
(2)160天后,标普500指数为1204.10点,新的利率期限结构如下表所示:
| 期限 | 即期利率 | 折现因子 |
| 20天 | 5.44% | 0.9970 |
| 200天 | 6.29% | 0.9662 |
| 380天 | 6.79% | 0.9331 |
| 560天 | 6.97% | 0.9022 |
计算该投资者的互换合约价值。
首先,计算美元固定利率债券价格。假设名义本金${F^ * }$为1美元,160天后固定利率债券的价格为:
$B_{fix}^* = C \cdot \left( {{D_1} + {D_2} + \cdot \cdot \cdot + {D_i} + \cdot \cdot \cdot + {D_n}} \right) + {F^*} \cdot {D_n}$
$B_{fix}^* = 0.0315 \times \left( {0.9970 + 0.9662 + 0.9331 + 0.9022} \right) + 1 \times 0.9022$
$B_{fix}^* = 1.0219$(美元)
其次,计算权益部分的价值:
$V_{equity}^ * = \frac{P}{{{P_{\left[ 1 \right]}}}} = \frac{{1204.10}}{{1150.89}} = 1.0462$(美元)
最后,由于合约名义本金为100万美元,则对于该投资者来说其价值为:
${V_{swap}} = {V_{equity}} – {B_{fix}} = \left( {V_{equity}^ * – B_{fix}^ * } \right) \cdot F = \left( {1.0462 – 1.0219} \right) \times 100 = 2.4334$(万美元)